Infinite divisibility or the lack thereof. A concept that appears in philosophy, physics, economics, order theory and probability theory. As early as the 5th century BCE philosophers, Leucippus and Democritus, were theorizing a world of divisible matter beyond our human senses. The Indian philosopher Maharshi Kanada proposed the concept of Atomism sometime between the 6th and 2nd century BCE. Aristotle proved that both length and time are infinitely divisible in his books of Physics in the 4th century.
The concepts of infinity and divisibility are not new, but they are fascinating, as is the discussion in relation to Bitcoin. Can something that is infinitely divisible can be considered scarce.
“I have done a terrible thing: I have postulated a basic building block of the universe that is infinitely divisible.”
Khalid Masood
Conceptual Finiteness
Finite means having a limit or end. It’s the opposite of infinite, which means unlimited or endless. Simple concepts. In mathematics you have the concept of a Finite Set. A series of numbers that have a start and an end, the number of elements in the set is its cardinality. The human expression of cardinality has been recorded as early as 40,000 years ago, equating the size of a group with recorded notches or a representative collection of other items, such as sticks and shells. Human beings have been counting and quantifying for a long, long time.
The concept of finite in the physical world applies to many things. On Earth we have a finite amount of resources, we have definable scarcity and known limits. In epistemology and information we have defined boundaries within finite systems. This scarcity and finiteness can, and does, lead to new approaches in knowledge acquisition and organisation. Focusing on understanding the system’s limits and maximising knowledge within those constraints.
We see complex and unpredictable emergent properties within finite systems that arise from the interactions between individual components. In biology we have protein folding and flocking behavior. In economics we have market bubbles emerging as unpredictable collective outcomes from seemingly rational individuals. We also have finite mathematical models like the Game of Life generating surprisingly complex and dynamic patterns within the bounds of simple instructions.
We also see this in neural networks where interconnected nodes learn simple rules but manage to develop complex patterns and novel solutions to complicated problems through co-operation. In physics we see examples in crystal formation where perfect and symmetrical structures arise from the interactions of individual atoms, illustrating how simple local rules can lead to complex global order.
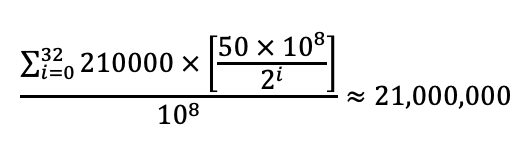
21 million is a finite number in a natural number set. This is the upper bound of the supply of bitcoin as defined by the issuance schedule. Bitcoin, by definition, is demonstrably finite.
Divide by ∞
The symbol for infinity was first used mathematically in the 17th century by John Wallis. Although it has a history of other uses. In mathematics it often refers to potential infinity rather than actual infinity. Confused yet?
“The continuum actually consists of infinitely many indivisibles”
Galileo Galilei
I will set aside the concepts of metaphysical infinity and physical infinity for the time being and focus on the concept of mathematical infinity. I will also pass on going into Ordinality and deal primarily with Cardinality as mentioned previously. Cardinality deals with the size of sets. We have already defined the natural number set of bitcoin as being 21 million (or as near as makes no difference – Further reading). Or, as some will point out, 2.1 quadrillion Satoshi’s, of which there are an attributable 100 million per bitcoin.
Given that bitcoin is computer code based on mathematics we have the ability to alter it to either expand the upper bound of the natural number set (dilution) or to further subdivide the individual units (division). For example, we can change the denomination from 1 Satoshi, to 1.0 Satoshi, allowing that single unit to be divided into tenths. If we apply an economic value to 1 Satoshi of $1, we now have the ability to distribute the whole into ten parts of 0.1 Satoshi each worth ten cents. As a whole they are still worth $1, but now can be held by ten different owners. This can be continued indefinitely, further dividing the units.
This is actual, rather than potential infinity. This could be continued forever as proved by the cardinality of the continuum as proved in Set Theory. Where between any two real numbers a < b, no matter how close they are to each other, there are always infinitely many other real numbers (Georg Cantor).
Given the proof of actual infinity, bitcoin can be subdivided into an infinite number of small units and still remain as part of a defined cardinal number set.
Factoid: the smallest infinite cardinal unit would be represented by 

The Economics of Scarcity
The concept of scarcity is one of the foundations of economic theory, but with multiple definitions and interpretations. It refers to the gap between definably limited resources and theoretically limitless wants. The notion that there is never enough of ‘something’ to satisfy all of the conceivable human wants even with our advanced technological ability.
“Humans want what they can’t have.”
Lionel Robbins
In more classical economic theory we can have two definitions of scarcity, that which is absolutely scarce, and that which is relatively scarce. Absolutism in scarcity is something that Thomas Robert Malthus laid out in 1798 in his book ‘An Essay on the Principle of Population. This posits that there is a finite ability for populations to support themselves with basic human requirements once it reaches a certain level of exponential population growth, leading to a collapse (Malthusianism). Absolute scarcity in this scenario is the condition where human requirements are outstripping the available quantities of required goods for survival.
Relativism in scarcity deals with the condition where multiple human requirements are greater than the available quantities. It deals with this mismatch between ‘what I want’ and ‘what I have’. The ‘have’ being money, time energy or ability. You can tie this into the concept of Economic Goods, items that satisfy our wants, provide utility, a product, or a service. A good is is an ‘economic good’ if it is useful to people, but has scarcity in relation to its demand. Such that human effort is required to obtain it. In contrast you have the concept of ‘free goods’, such as air in the atmosphere, or the earth under our feet. Something that is so naturally abundant that most of us need no conscious effort to obtain them.
A scarce good in modern economics is considered something that has more quantity demanded than quantity suppled, at a notional price of zero (Supply & Demand). We can also define goods as having relative levels of scarcity.
- Demand induced
- Supply induced
- Structural scarcity
Demand induced scarcity happens when the demand for a resource increases, but the supply remains static. Supply induced scarcity happens when supply is low in comparison to the demand. Structural scarcity is a function of access, either geographically, politically or environmentally.
On the opposite side of the definition are non-scarce goods. Not those that are necessarily valueless but that are so abundant they satisfy all the needs and desires without competition. It must either be infinite, have properties whereby no one would be able to hoard or monopolise the supply, or that it can be infinitely replicated.
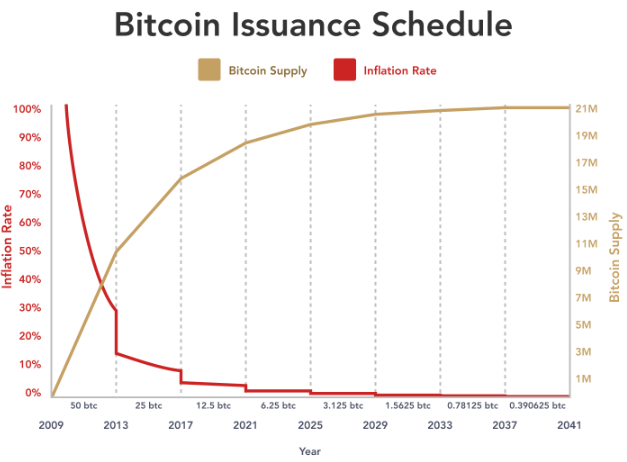
With bitcoin we have to understand that there are dynamics within all of these definitions that we try to apply to it as an asset. While people buying bitcoin are the demand side of the equation, miners are also demand side, not supply side. Miners are competing with resources, traders and buyers are competing with fiat. The supply side scarcity is pre-determined based on the rewards issued per 10 minute block, which halves every 4 years, ultimately ending at just under 21 million in the year ±2140.
Structural scarcity with bitcoin doesn’t exist beyond someone’s ability to access the internet. There are artificial limits imposed by banking and governments that constrict accessibility, but more, the structural scarcity is indicative of how early it is in an adoption S curve.
Value fluctuation (volatility in fiat price), as a result of supply and demand, happens at the margins of the supply, not on the whole. That which is available for exchange at any one point in time for sale sets the market value. Defense of the volatility usually comes from the opinion that we as human beings have never had to price a definably finite asset before, but more than that, we’ve never monetised an asset, that still defies common understanding, from zero value, in such a short period of time.
Conclusion
Whether an asset, or a good, with a non-zero economic value and infinite divisibility, can be considered scarce, is a complex question. Much debated, and with no broad consensus. It is entirely subjective on how you define scarcity.
Scarcity arises not just from quantity, but from demand exceeding supply. If demand remains high for individual units, despite their small value, it could create effective scarcity due to competition and price fluctuations. As more miners join the network in competition, this only increases the demand side of the equation.
Even with infinite divisibility, the totality of the asset (or number set) can still be finite, scarce and valuable. For example, imagine a single “Master Key” asset worth $1 million, infinitely divisible into “subkeys” with a theoretical aleph-null zero bound individual value. The Master Key would still be scarce, despite any subkeys created.
On the counter argument, division could create an over-reduction in individual values proportionate to the sum of the whole. It may reach a point where each sub-unit holds no practical economic value, negating the concept of scarcity entirely. If the good is also no longer deemed desirable this also affects the demand side of the equation.
Currently 1/100,000,000th of a bitcoin (1 Satoshi) is worth 0.000169 USD (Jan 2024). You wouldn’t stoop down to pick that up off the street. But if it was worth $1, you might. Arbitrarily dividing something valuable into infinite sub-units is not worthwhile until the sum of the whole reaches a certain economic value, what that is, I’m not sure.
Bitcoin doesn’t neatly fit into any category of goods in traditional characteristics. Perhaps the reason why so much is written about it. It shares characteristics with Monetary Goods due to its fungibility, divisibility, potential as a medium of exchange and long term store of value. It also shares aspects with Consumable Goods. Whilst not physically consumed its utility can be ‘spent’ through transactions and its use as liquidity and collateral also provide a level of consumption owing to the fact that it is held outside the liquid, tradeable quantities.
It is also an intangible or Digital Good in line with other digital media. Anyone can take a copy of the code and run a new example of bitcoin. Many have done in the past, changing minor aspects of the code as they see fit (BCH/BSV/ABC). In that sense, it is infinitely replicable. However, the bitcoin generated by those networks would be rejected by the original, and thus some of the value relies on the network effect of an already established community and the computing power behind it.
Bitcoin is finite and infinite. It is a scarce good, yet everyone can have a piece of the pie. It is infinitely replicable by anyone, yet entirely unique.
It’s a grey area.
For a primer on Bitcoin, wealth, and inequality: Chpt 24.1: Profit Margin



One thought on “Chpt 29: Grey Area”